著書「生産システムの進化論」の中で、トヨタ生産システムの分析にあたって著者;藤本隆宏氏は、「進化論的な発想に基づき」、「筆者の専門である技術・生産管理のプロセス分析をドッキングさせる」という分析枠組みを設定した。ところが著者の専門の中枢にあるはずの“生産リードタイムを記述する数式”は「文系的な表現であり、数式がそのまま使えるという話ではありません」との説明。
生産ラインの重要な特性が盲点に入っているのではないか。だとすれば、進化論分析の要とも思われる「技術・生産管理のプロセス分析」は機能するのかどうか、怪しくなってくる。
生産ラインの重要な特性とは、どのような特性なのか。分析に及ぼす影響はあるのか、ないのか。影響があるとしたら甚大なものなのか、些細なことなのか。いずれにしても、先ずはその特性を理解する必要がある。
ということで、生産ラインの生産リードタイムに関連する重要な特性、特徴について概覧するため、ちょっと寄り道することをご容赦いただきたい。
1,ひとつの工程からなる生産ラインの基本特性
1.1 1工程の特性
生産ラインは、構成するいくつかの工程の繋がりで成り立つ。生産リードタイムは、ザックリといえば、工程ごとの待ち時間と処理時間の総計である。先ずここでは、1つの工程の、主に生産リードタイムに関する特性に注目してみる。処理時間は、古くはテイラーの時代から加法性があることが知られているが、待ち時間についてはわからないところが多い。つまり、生産リードタイムの挙動を理解するためには、待ち時間の理解を深める必要がある。
図1にワーク(被処理物、オーダー、、)が1つの工程を流れる様子を示す。
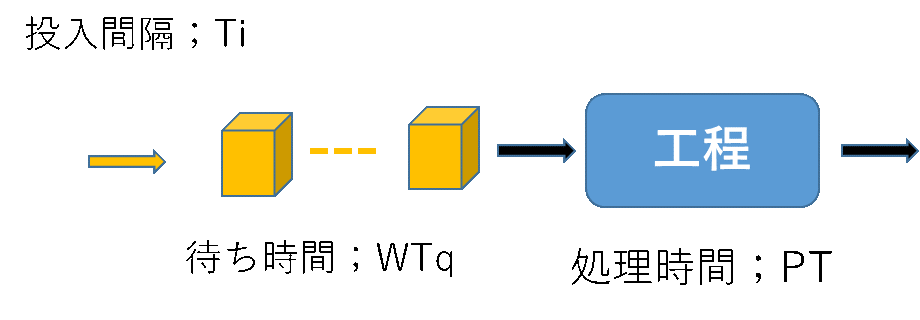
図1 1工程の流れ
1.1.1 投入間隔、処理時間が一定の場合
工程にワーク(オーダー、被処理物)が投入される。工程が手空き状態であればワーク到着と同時に処理を開始する。工程がビジーなときは工程が処理可能になるまでワークは待つことになる。このような動きを捉えるために、4つの変数を定義しておく。
- 投入間隔;Ti 工程にワークが投入される(到着する)時間間隔
- 処理時間;Tp 工程の処理時間(作業時間、加工時間等)
- 稼働率;ρ=Tp/Ti
- 工程前で待つ時間;WT
先ず。Tp、Tiが一定値(バラツキなし)の場合を考えてみる。立ち上がり期間は除き、流れが一定となる定常状態を想定する。
ρ≤1では工程前で待つ時間WTは0。完成時間間隔はTiと同じ。ρ>1では時間経過とともにWTが長くなり、ρが大きければ大きいほど急激に長くなるが、完成時間間隔はTpと同じ。まとめると次のようになる。
Ti、Tpが一定値の場合、WTは次のようになる。
- Ti≥Tp(ρ≤1) WT=0、完成時間間隔=Ti
- Ti≤Tp(ρ>1) WTは時間経過とともに階段状に長くなる、完成時間間隔=Tp
ρ=1を境にWT、完成時間間隔の挙動がまったく異なることに留意しておきたい。
1.1.2 投入間隔、処理時間がバラツク場合
実際の生産ラインではTiもTpもばらつく。それぞれのバラツキ(変動)を次のように定義する。
- 投入間隔平均;Ti 分散;Vti 変動係数;Sti
- 処理時間平均;Tp 分散;Vtp 変動係数;Stp
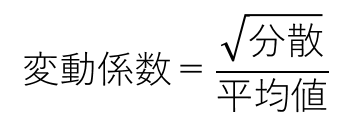
TiやTpがバラツク場合、待ち時間の挙動は意外に複雑である。シミュレーションで確かめてみるのがわかりやすい。シミュレーション・ソフトはいくつか市販されているが、ここではエクセルで簡易的に行う。エクセルでのシミュレーション結果とシミュレーション・ソフトの結果はほぼ一致することは確認している。
以下の数値を使ってシミュレーションを行う。
・処理時間平均;Tp=10、変動係数;Stp=0.1、0.5、0.9
・稼働率;ρ=0.7、0.9、0.99
・投入間隔;Ti=10.101、11.111、14.286、変動係数;Sti=0.1、0.5、0.9
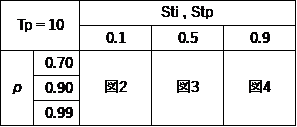
表1 シミュレーション条件
図2、図3、図4に表1に示す条件での待ち時間のシミュレーション結果を示す。尚、計算回数はそれぞれ3,000回(データ数;3,000)で、待ち時間0のデータは表示していない。
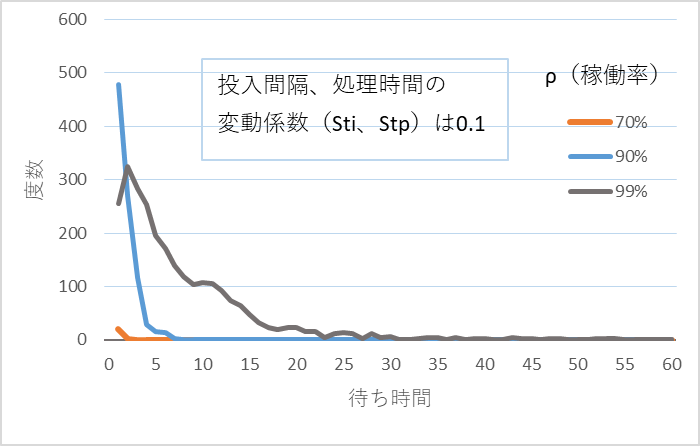
図2 待ち時間の分布、Sti、Stpは0.1
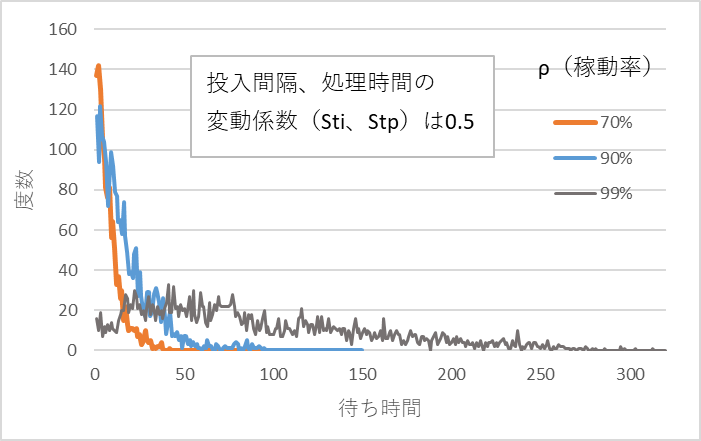
図3 待ち時間の分布、Sti、Stpは0.5
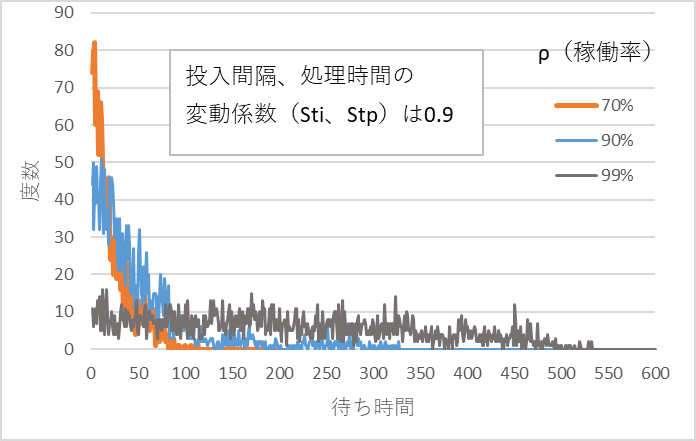
図4 待ち時間の分布、Sti、Stpは0.9
3つのシミュレーション結果から次のような特徴があることがわかる。
- 投入間隔、処理時間のバラツキが大きくなると待ち時間は長くなる。
- 稼働率が高くなると待ち時間は急激に長くなる。
- 待ち時間の分布形状は右方向(長くなる方向)にすそ野を引くように伸びて行き、中央値付近にピークはない。
1.2 数理モデルで表す
図1に示すような工程で発生するワークの待ち時間の特性を知るためには「待ち行列理論」を応用するのが一般的である。生産工程の特性をすべて記述することはできないが、待ち時間についてのメカニズムを理解する助けにはなる。
「待ち行列理論」では、投入間隔、処理時間の分布として、次の4つが指定できる。
- M・・・ポアッソン分布(投入間隔の場合)、指数分布(処理時間の場合)
- D・・・一定分布
- Ek・・アーラン分布
- G・・・一般分布(平均値と分散が既知、分布形状不問)
「待ち行列理論」の数理モデルは主に次の解を求める。
- 待たされる確率
- (処理中+待ち行列)平均ワーク数
- 待ち行列の平均の長さ
- 平均待ち時間
ここでは、分布形状はG、待ち時間平均を求める近似式を使ってみる。
待ち時間平均(WT)を記述する数理モデルとして、次の近似式が知られている。
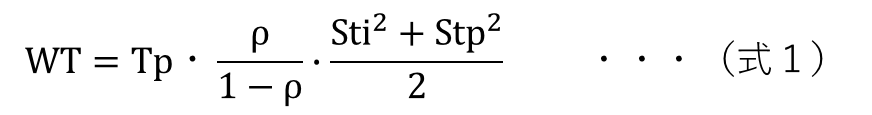
シミュレーションと(式1)を比べてみると、StiやStpが大きい領域、ρが高い領域では近似式で求めた値が大きく出る傾向がある。これは、近似式は定常状態(時間が経過しても変化がみられない状態)を条件としていることが影響していると思われる。シミュレーションにしても数式にしても、待ち時間平均を求める精度的限界があることに留意しておく。
ただ、(式1)は待ち時間の構造を理解するのに役立つ。待ち時間平均WT)は主に、投入時間平均(Ti)、処理時間平均(Tp)、投入間隔の変動係数(Sti)、処理時間の変動係数(Stp)で決まる。それぞれの影響度合いを視覚的にわかりやすく示せば、図5、図6、図7のようになる。
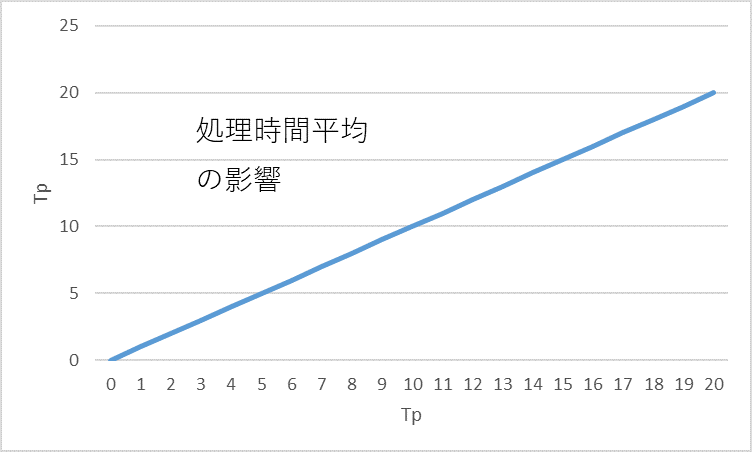
図5 処理時間平均の影響
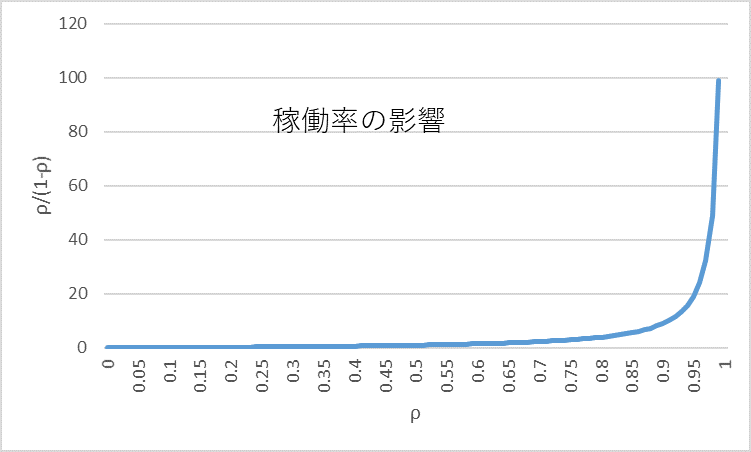
図6 処理時間平均/投入間隔平均(稼働率)の影響
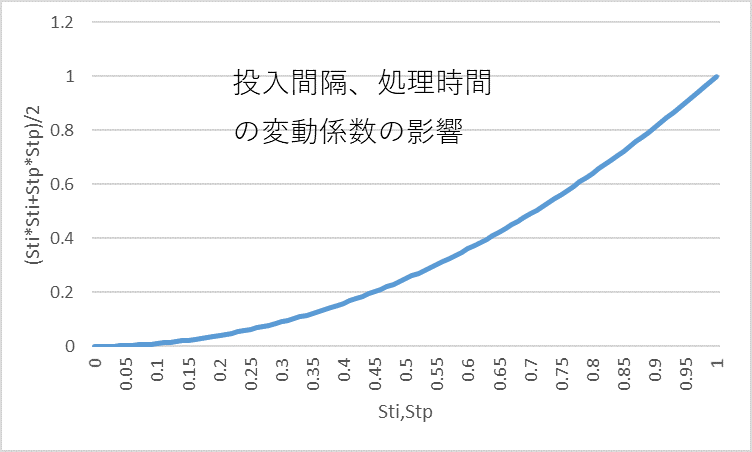
図7 投入間隔、処理時間の変動係数の影響
また図8に投入間隔、処理時間の変動係数が0.1、0.25、0.5、0.75、1のときの稼働率に対して待ち時間平均(処理時間平均を基準として)がどのように変化するかを示す。
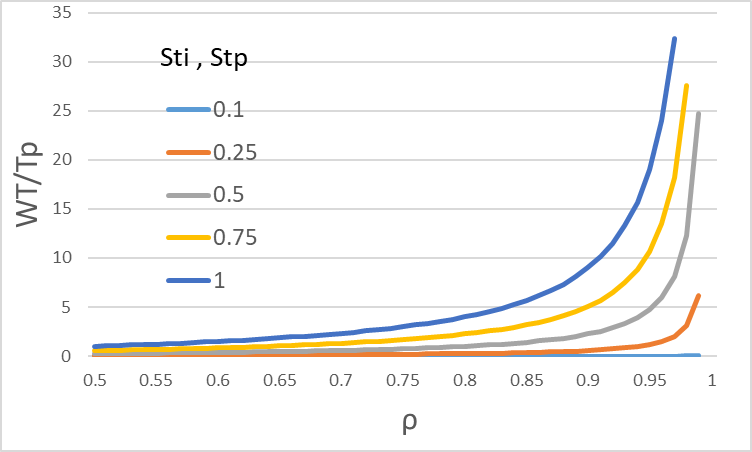
図8 稼働率(処理時間平均/投入間隔平均)0.5~1に対する待ち時間平均のカーブ
待ち時間平均(WT)を求める近似式(式1)からわかる待ち時間平均の特徴をまとめると次のようになる。
- WTは処理時間平均(Tp)に比例する。
- WTは稼働率(ρ)が100%に近づくに従い急激に長くなる。
- WTは投入間隔、処理時間の変動係数の自乗の和に比例し長くなる。
尚、待ち時間(WT)の分散を求める数式は、論文レベルの提案はいろいろあるが実用的なものは見当らない。
2,5工程からなる生産ラインの特性
一般的に生産ラインは複数の工程が繋がって構成されている。1つの工程での終了時間間隔が次工程の投入間隔となり、この関係が最終工程まで連鎖する。
実際は、1つの工程の終了時間間隔を求める実用的な数式も見当たらないし、工程が複数つながるとなれば、待ち時間の平均にしても分散にしても、簡単に数式で計算することは難しい。論文レベルでは多数発表されているようだが、実用的に使えるものはない。
2.1 シミュレーションで確認
シミュレーションで確かめてみることにする。前回と同様、エクセルで簡易的にやってみる。エクセルの結果とシミュレーション・ソフトの結果はほぼ同じことは確認済み。
図9に示すように、5工程の直列ラインで、工程B~Eの処理時間は10でどの工程も同じ。工程Aは工程B~Eの稼働率を設定するため処理時間平均は12.5(80%)、11.1(90%)、10.5(95%)の3種類。工程Aの投入は在庫から常時可能とし、工程A前で待つ在庫の待ち時間はカウントしない。生産リードタイム(フロータイム)は工程Aへの投入から完成までの時間。

図9 シミュレーションを行う5工程生産ライン
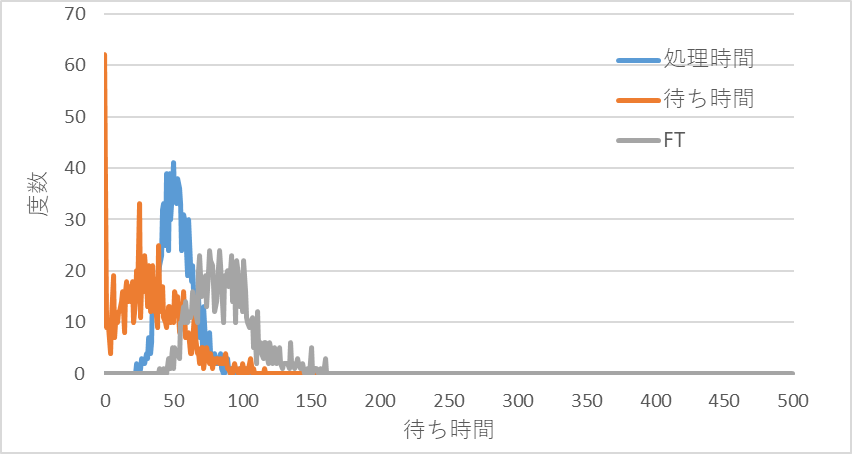
図10 稼働率80%での処理時間、待ち時間、フロータイム(FT)の分布
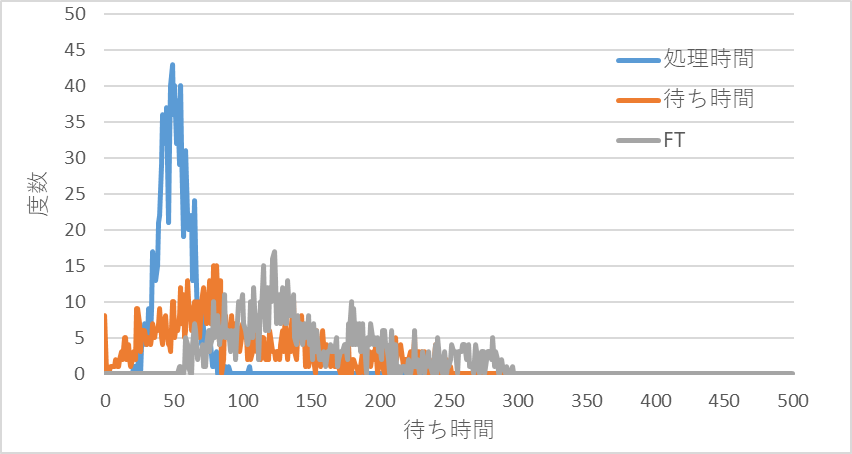
図11 稼働率90%での処理時間、待ち時間、フロータイム(FT)の分布
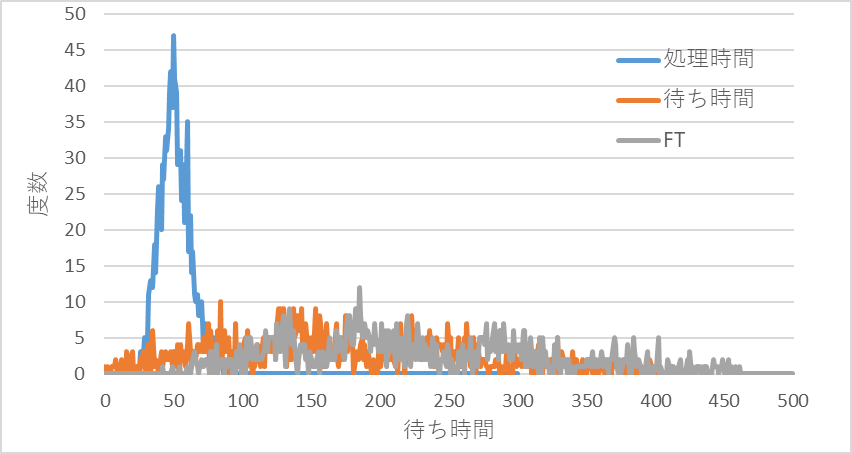
図12 稼働率95%での処理時間、待ち時間、フロータイム(FT)の分布
図10~図12に投入から完成までにかかった各工程の処理時間合計と待ち時間合計、およびフロータイム[FT=Σ(各工程処理時間+各工程待ち時間)]の分布を示す。FTは生産リードタイムに相当する。
この2つの条件を比べてみてわかる特徴を挙げてみる。
2.1.1 処理時間
処理時間の平均と標準偏差は、計算でも求めることができる。
計算例を示すと処理時間の平均は、次のようになる。
稼働率80%では;12.5(工程A)+10×4(工程B~E)=52.5
稼働率90%では;11.1(工程A)+10×4(工程B~E)=51.1
稼働率95%では;10.5(工程A)+10×4(工程B~E)=50.5
処理時間の標準偏差は、次のようになる。
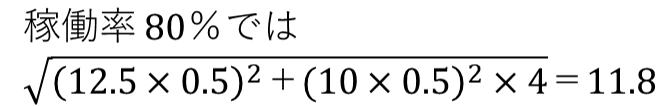
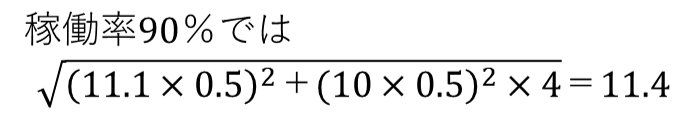
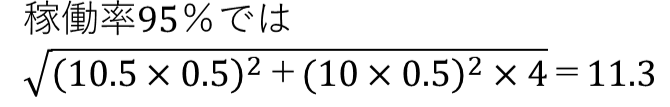
処理時間は加法性があり、比較的簡単に計算で求めることができる。付記しておきたいことは、待ち時間の長短にかかわらず、つまり、待ち時間がゼロでも100でも、上記の特性は成り立つことである。
2.1.2 待ち時間
待ち時間の平均値を求める式は、投入間隔および処理時間の分布形状が既知で(指数分布、一定分布、一般分布、アーランK分布)、定常状態(時間が経過しても変化ががみられない状態)を仮定してしているため、実際の生産ラインに適用できる範囲は限られている。(詳細は待ち行列理論を参照)
待ち時間の分布の特徴は、待ち時間が短いときは、待ち時間が0の度数が多く、その近くに小山状に分布するが、待ち時間が長くなるとなだらかな丘陵状や低く広い台地状に分布する。また、ρが高い領域とかStiやStpが大きいときは、定常状態を安定的に再現できないためか、シミュレーションを行うごとに異なる分布形状となりやすく、特定しにくい。
また、ρを特定するためにはある時間間隔が必要であり、時々刻々の瞬時のρを知ることはできない。複数工程が繋がる生産ラインの待ち時間の平均、分散を求める計算式は、限定的な条件でしか使えないものばかりで、実用的に使える計算式は見当らない。。
分布形状が既知で釣鐘状(山状)であれば、統計的処理をして確率で判断することもできそうであるが、待ち時間に関しては分布形状が低く広く且つ不安定であるため、統計処理が限定されることに留意する必要がある。
2.1.3 稼働率と待ち時間の関係
図8を再掲し、稼働率(ρ)と待ち時間(WT)の関係を示しておく。図は1工程の特性であるが、工程が複数連なる生産ラインでも同様の特性を示す。一般的にできるだけ高い稼働率を狙うが、実際は70%~90%ぐらいの範囲で行われることが多い。この範囲は稼働率が少し上がるだけで待ち時間が急激に長くなる不安定領域であり、生産管理が混乱する要因となる。

図8(再掲) 稼働率vs待ち時間
2.1.4 まとめ
生産ラインで発生する待ち行列現象の特徴を簡単にまとめておく。
- 待ち時間は稼働率に対して指数関数的に長くなる。
- 瞬時瞬時の稼働率はわからないので、稼働率vs待ち時間平均のカーブが既知でも待ち時間平均を求めることは難しい。
- 「定常状態」を現実的に確認することはできない。
- 待ち時間の平均の近似式はあるが、分散(バラツキの大きさ)を求める実用的な式は見当らない。
- 待ち時間の分布は平均が長くなるとなだらかに広がり且つ不安定になるため、統計的な予測が難しくなる。
- シミュレーションによる予測も、同じ理由で、難しくなる。
- 待ち時間の異常値を検出するためには、待ち時間の分散がある一定以下となる条件を設定しなければならない。
3,生産方式と待ち時間との関係
生産ラインで発生するワークの待ち時間は生産リードタイムを大きく左右する。その待ち時間は、生産方式や生産管理方法によってどのような違いがあるのか、概観しておく。尚、このテーマについては、別紙面で詳細に後述する予定である。
- フォード方式(ベルトコンベアー方式)
フォード方式はワークをベルトコンベアーで移動しながら作業が行われることを基本とすれば、滞留はなく、待ち時間は発生しない。ただ、様々な使い方があるので、基本形として、待ち時間はゼロと考えておく。
- MRP
同種の製品をまとめてつくるので、生産工程間で発生する待ち時間は短いが、ロット生産のためにロットの大きさにほぼ比例した在庫の滞留(待ち時間)が発生する。但し、待ち時間はほぼ生産ロットの大きさで決まるので、滞留する在庫数やその待ち時間は計算可能である。
- 多品種変量生産
多様化が進む現代の生産環境では、中小企業だけではなく大企業も含めて、大部分の製造現場が多品種変量生産となっている。具体的には、見込・受注混合生産となる工場が多く、待ち時間が不安定に発生する領域でのオペレーションとなりやすい。生産管理システム(ツール)を導入し管理の安定化に努めるが、予期せぬ変動に対応は追い付かないのが現状。改善策も出尽くす中、日常業務を仕切るのは経験豊富なベテランの経験則。捉えにくい待ち時間も1工場に限れば特徴が出てくる。それを経験則として学習したベテランが現場を支えている。
- トヨタ方式
平準化、作業標準の徹底、ムダ取り、多能工、アンドン、、、等で投入間隔、処理時間のバラツキを抑え、稼働率が高い領域でも待ち時間の長大化を防いでいる。トラブル(品質、待ち時間異常等)が生産ラインの管理状態を不安定にする恐れがあるときはラインをストップする仕組みもある。
Just In Time は正に、待ち時間の発生を抑える仕組みであると言える。
4,生産型とプロジェクト型の違い
「良い設計の良い流れ」という切り口でみると、設計業務の待ち行列現象についても追記しておく。生産ラインの流れを生産型、設計業務をプロジェクト型と分けて、比較してみる。
図13に示す事例で試算してみる。できるだけ同じ条件で比べた方がわかりやすい。生産型もプロジェクト型も直列5工程(5タスク)、処理時間平均は工程4(タスク4)が9時間、他の工程(タスク)は7時間とする。生産型の工程バラツキは変動係数0.25、プロジェクト型は0.75と大きくしてある。生産型のオーダはランダムに投入されるが、平均時間間隔は10時間。プロジェクト型はプロジェクトX、ひとつ。
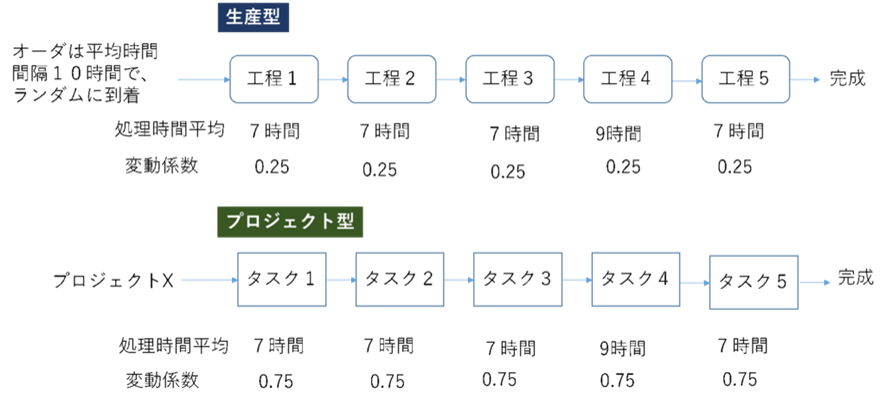
図13 生産型とプロジェクト型の比較
生産型では、ひとつのオーダが完成するまでの時間、プロジェクト型ではプロジェクト開始から完成までの時間をシミュレーションしてみる。その一例を図14に示す。
プロジェクト型のタスクのバラツキは生産型のそれの3倍であることに留意。にもかかわらず生産型の所要時間の方が平均も最大値も長くなっている。分布をみても、プロジェクト型は、正規分布に近い分布形状だが、生産型のそれは右に大きくすそ野が伸びている。生産型では待ち時間が発生するのに対して、プロジェクト型は発生しない(小さい)ことが原因である。
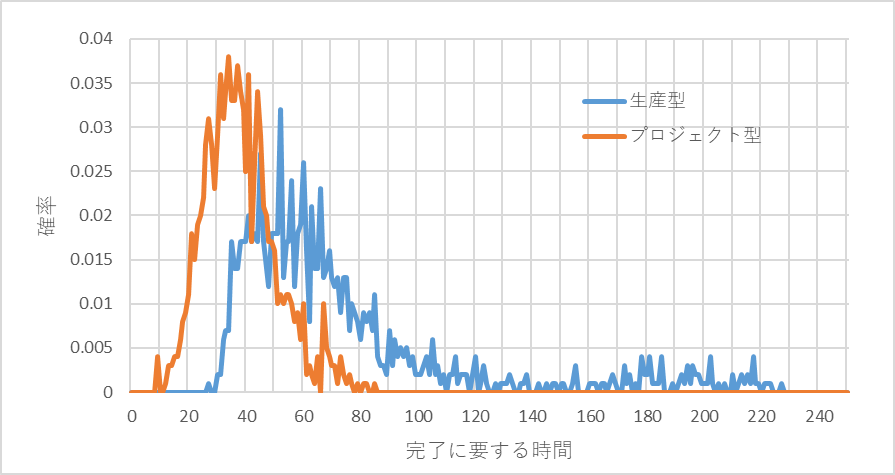
図14 生産型とプロジェクト型の完成までの所要時間の比較
プロジェクト型が待ち時間の発生が小さいのは、生産型が工程のリソース(機械設備、作業員等)が固定されていて、そこに多数のタスク(被処理物、ワーク、ジョブ、、)が流入するのに対して、プロジェクト型は予め決められたタスクにリソース(人)が割り当てられていく、というタスクとリソースの関係の違いで説明できる。
巷ではプロジェクト管理ソフトは使えるが生産スケジューラは使えない、という話がささやかれている。同じ理由である。
5,「生産システムの進化論」に戻って
「生産システムの進化論」が分析枠として設定した「筆者の専門である技術・生産管理のプロセス分析をドッキングさせる」という狙いの中核をなす生産リードタイムを構成する主要な特性が見逃されていた。棄却された生産ラインの特性とは、待ち行列現象によるワーク(被処理物、オーダー)の待ち時間である。待ち時間は、稼働率を高くすると、処理時間の数倍、数十倍の長さに簡単になる。程度の差はあれ、すべての工程で起こりえる現象である。この影響は軽微である、といえるだろうか。
「生産システムの進化論」に戻って、書の分析過程を追ってみることにする。